If we design an algoritmh and we stop thinking about CPU time and focus our attention on main bottleneck of “computer speed”, we have to fucus our attention on IO access in (main) memory. Moreover this introduce new problem, how to optimize access in memory?

If I design a mergesort algorithm, I’ll find useful to build a k-way mergesort where the complexity decrease when the run size increas [1]. So it’s useful to find a way to create a sorted run as long as we can.

We can use some tecnique, one of them called Algorithm R (Replacement selection) by Knuth [2], or, more funny, the snowplow algorithm. It outputs a sorted runs of size greater that M (memory size), with average size equal to 2M and then you can use this sorted runs as input in a (k-way) mergesort.

Step 1

First of all you need to create an min heaptree with M element in main memory. This tree can be build in O(n) time.

Step 2

Get an element e from unsorted set (saved in external memory), and then compare it with the minimum element m extracted from min-headtree.

Case 1

If the element is less then extracted one, i.d. e < m, then put e in unsorted bucket in main memory and send e to output.

Case 2

Else if the element is greater than the minimum, i.d. e > m then send m to output and add new element e in heaptree then heapify the tree - O(log n)

Step 3

If heapTree is empty

• build a new heaptree with unsorted element put in main mamory bucket -(notice that if heaptree is empty, the unsorted bucket contains M-1 elements)

else

• back to First Step

If the external sorted elements in external memory ends, extract min from min-headtree until it became empty.

Example

Here I provide a small example to show how this algorithm works.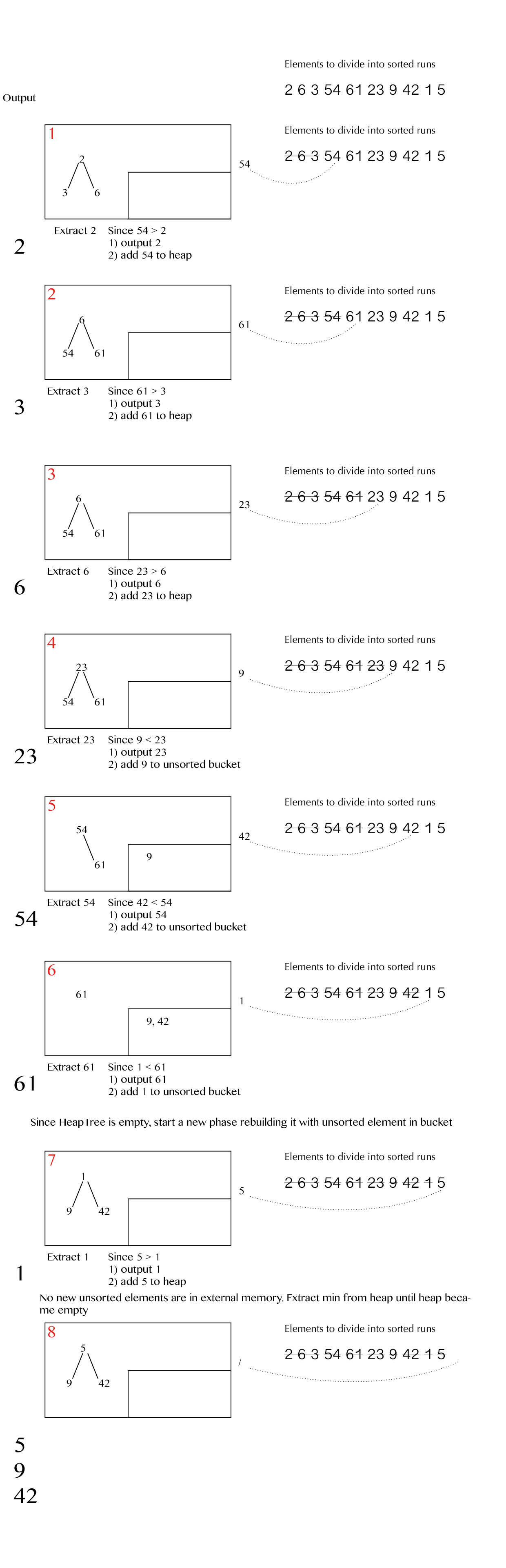

So the sorted runs are:

• 2 3 6 23 54 61
• 1 5 9 42

Conclusion

As Ferragina says on [1], Snow-Plow builds O(n=M) sorted runs, each longer than M and actually of length 2M on average. Using Snow-Plow for the formation of sorted runs in a Merge-based sorting scheme, this achieves an I/O-complexity of \( O(\frac{n}{B}log_{2}{\frac{n}{2M}})\) on average.

References

[1] The magic of Algorithm, lecture notes of Paolo Ferragina

[2] Donald E. Knuth. The Art of Computer Programming: volume 3. Addison-Wesley, 2nd Edition, 1998.