Dopo aver visto nella prima parte come scambiarsi una chiave senza doverla comunicare in chiaro, abbiamo visto nella seconda parte come è possibile scambiarsi messaggi cifrati senza neanche doversi scambiare una chiave, tramite l’uso dell’RSA.

Lo scopo di oggi è vedere come sfruttare l’RSA, o qualsiasi altro algoritmo di cifratura asimmetrico, per verificare l’identità di un mittente come se lui lo avesse firmato.

La firma digitale

Bob mi manda un messaggio: “Il pagamento puoi effettuarlo al seguente IBAN: IT000….001”. Ed ecco il problema, come verifico che quel messaggio sia stato spedito effettivamente da Bob e non sia stato intercettato da qualcuno che ha prontamente modificato l’IBAN con il suo?

Di certo non è cifrando il messaggio che risolvo la cosa poichè cifrando qualcosa lui è in grado di verificare che solo io possa leggere il messaggio ma io non sono in grado di verificare chi abbia spedito il messaggio.

Recap

Come avevamo già visto, ogni utente in un sistema di crittografia asimmetrica dispone di due chiavi: la chiave pubblica e la chiave privata. La caratteristica è che la chiave pubblica può essere liberamente comunicata a chiunque e la chiave privata invece rimane segreta. Inoltre, il legame tra queste due chiavi è che, applicando prima una e poi l’altra al messaggio, il testo viene cifrato e decifrato, potremmo dire che sono una l’inverso dell’altra. In formula, sia C(m, k) l’algoritmo usato, m il messaggio e k la chiave usata:

\[ m = C(C(m, k_{pu}), k_{pr}) = C(C(m, k_{pr}), k_{pu})\]

Come firmare un messaggio

Per firmare un messaggio dobbiamo quindi trovare un modo per sfruttare cifrare il messaggio in un modo che solo il reale mittente potrebbe fare.

La cosa che potrebbe certificare il mittente di essere Bob è il dimostrare di conoscere la sua chiave privata, \( k_{pr-B}\). Certo, Bob non può però rivelare al mondo (altrimenti non sarebbe più privata) questo dato e quindi escogita un modo che trovo geniale: usa l’algoritmo di cifratura al contrario, invece che cifrare con la chiave pubblica del ricevente, cifra con la sua chiave privata. Chiaramente tutti saranno in grado di “decifrare” il messaggio, basterà applicare la chiave pubblica di Bob. Il nostro scopo infatti, vi ricordo, non è cifrare il messaggio ma fare in modo di verificare l’identità del mittente.

Cosa comporta questo? Che il messaggio è cifrato con una chiave che solo Bob può conoscere e di cui tutti sono in grado di verificarne la correttezza poichè tutti conoscono la chiave pubblica di Bob e quindi, dato che una è “inverso” dell’altra, è possibile effettuare \( m = C(C(m, k_{pr}), k_{pu}) \).

Abbreviare il messaggio: hashing

Certo che però cifrare un intero messaggio che spediremo anche in chiaro (il nostro scopo ora infatti non è di spedire il messaggi cifrato, avevamo già visto come fare per quello, ma di spedire un messaggio e autenticarlo) vuol dire raddoppiare la quantità di dati da spedire e calcolare il messaggio cifrato su una grande quantità di dati inutilmente.

Se poi ci mettiamo anche il fatto che gli algoritmi di cifratura asimmetrica sono molto più complessi da un punto di vista computazionale dei classici algoritmi a cifratura simmetrica, per fare un esempio una password lunga 2048 bits usata in un cifrario RSA viene, da un punto di vista di sicurezza, comparata ad una lunga solo 128 bits in un cifrario AES (uno dei più usati cifrari simmetrici in circolazione)… ecco che tutti risulta inefficiente!

Come aggirare il problema? Non viene di solito cifrato il messagio completo ma una sua sintesi, l’output cioè di una funzione hash, h(m).

Cosa è una funzione hash?

Ecco, questa cosa è forse un po’ tecnica e si discosta un po’ dal mood di queste pagine che volevano essere una cosa generale da far capire a tutti. Tuttavia provo a lasciare le cose più semplici possibili, decidete voi se lo sono abbastanza da leggerle.

Una funzione hash è una funzione che, dato in input un qualsiasi messaggio (stringa di bits di qualsiasi lunghezza), restituisce in output una serie di bits di lunghezza fissa. Chiaramente questa cosa comporta che vi sono moltissimi (leggasi infiniti) messaggi che possono corrispondere ad uno stesso hash, cioè: \[ \exists i, j \ s.t.\ h(i)=h(j) \]

Tale affermazione è abbastanza intuitiva, infiniti inputs, finiti possibili outputs, infiniti inputs collideranno per il pigeonhole principle.

E allora? E allora si cerca di usare funzioni hash abbastanza casuali tali che due input simili non presentino lo stesso hash o, ancora meglio, questo hash sia molto differente. Facendo un esempio, potremmo usare una famosa funzione hash, la SHA-256:

sha256("ciao a tutti") = d866234a1931e169288df6353923629cb4297c299da5fdfbe00b7fa42861eb98
sha256("ciao a tutte") = 41a0afdbed24669aad1da115f0e8577277a41ec351ac6a6c7169a8e6f28b7084

Un’altra caratteristica di queste funzioni, per la loro natura dimensionale (infiniti input, finiti output), è che non sono invertibili. Se vi dessi quindi l’output d866234a1931e169288df6353923629cb4297c299da5fdfbe00b7fa42861eb98 non sareste in grado di capire quale input lo ha generato (avreste infiniti input tra cui scegliere).

Come funziona la firma

L’idea, per tornare ai nostri scopi, è di per sè molto semplice: mandare due valori, il messaggio in chiaro e l’hash del messaggio cifrato con la chiave privata

\[ <m, C(h(m), K_{pr-B})> \]

Un eventuale ricevente non deve far nient’altro che prendere la chiave pubblica di Bob, e applicarla al secondo componente spedito. Se il procedimento è andato a buon fine il risultato sarà \( <m, h(m)> \). Basterà quindi calcolare l’hash di m e confrontarlo con il risultato della decifratura.

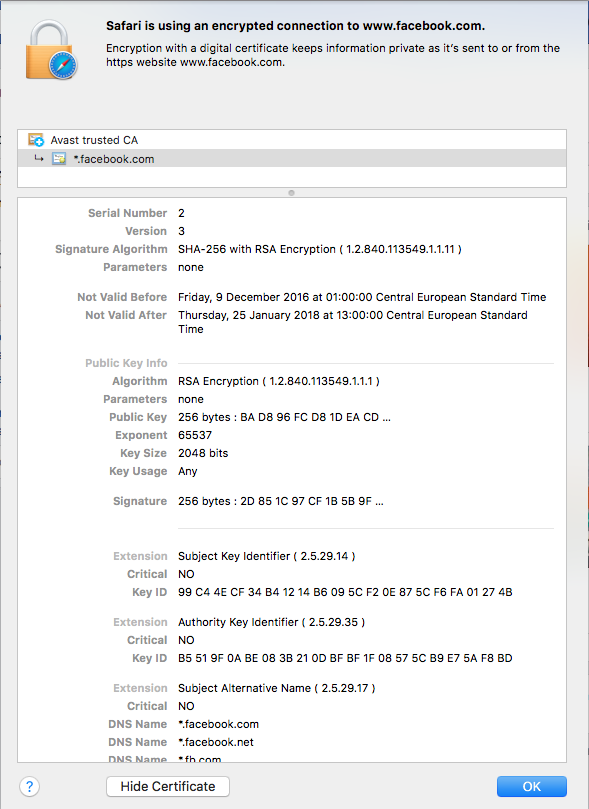
Il problema della verifica della chiave pubblica

Si introduce, in tutto questo ragionamento, un problema che, quando abbiamo introdotto i cifrari asimmetrici, avevamo ignorato.

In altre parole, come verifico che nessuno abbia sostituito la pagina dove Bob ha scritto la sua chiave pubblica con una pagina contenente la sua per validare lui un “finto” messaggio?

Chiaramente come possiamo immaginare si è trovata una soluzione anche a questo e viene usata in maniera consistente ogni qual volta navighiamo in https sul web. Sono stati creati delle certification authority che si fanno carico di certificare la validità delle varie chiavi pubbliche. Se voglio che tutti siano sicuri che la mia chiave pubblica è \(k_{mia}\), me la faccio certificare da una certification authority che si salverà \(k_{mia}\) e la comunicherà corretta a chiunque la richieda.

A questo punto si torna alla domanda con cui avevamo aperto questa serie di articoli sulla crittografia, chi certifica la Certification Authority?

Beh, in tal caso diciamo che si autocertificano, o meglio, per capirlo bisogna capire in che scenario si utilizzano. Quando navighiamo noi usiamo un browser che si connetterà in maniera cifrata a vari server verificando l’identità di ognuno di questi leggendo la chiave pubblica dichiarata (la questione è un po’ più complicata ma cerchiamo di lasciarla più semplice possibile). A questo punto, si connette alla certification authority per controllare la validità. Questa connessione che effettua avviene con il metodo di cifratura asimmetrica visto nella seconda parte e, la chiave pubblica della c. a., il browser la conosce perchè ce l’ha salvata nel suo database locale. E chi l’ha inserita in quel database? Diciamo che il programmatore potrebbe aver inserito le principale c.a. e quando scaricate il browser ve le ritrovate già lì pronte, e poi a cascata tutte le altre.

Per vedere tutte queste cose, sui siti che visitate, basta cliccare sul lucchetto posto, solitamente, alla sinistra dell’url nella barra degli indirizzo. Vi dovreste ritrovare una schermata simile a quella mostrata nell’immagine qui sopra con tutti i dati di cui abbiamo parlato oggi che ora, spero, sarete in grado di capire un po’ meglio.